티스토리 뷰
Big-O Notation이란?
- 알고리즘의 효율성을 수학적으로 표기
- 알고리즘 효율성 -> 데이터의 개수(n)이 주어졌을 때 기본연산 횟수를 의미
- 시간 복잡도와 공간복잡도를 나타내는데 주로 사용
(시간복잡도 : 알고리즘의 시간 효율성, 공간복잡도 : 알고리즘의 메모리공간 효율성)
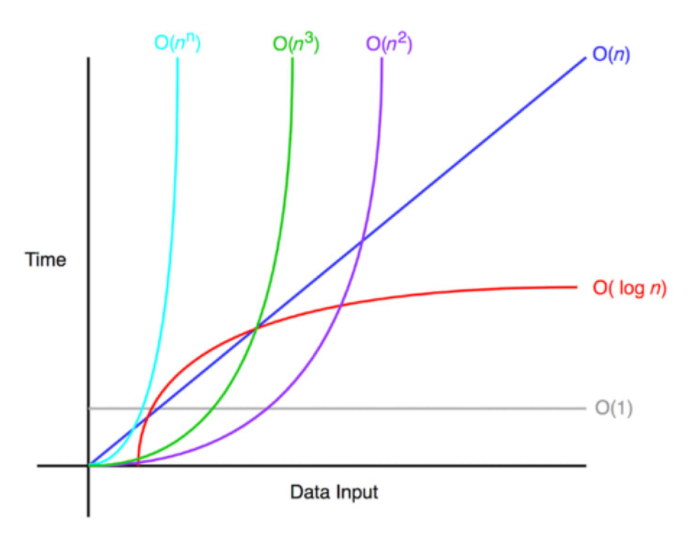
시간 복잡도의 성능 비교 (왼쪽에 위치할수록 효율성이 높음, 최악의 경우를 기준으로 알고리즘의 성능을 판단함)
O(1) > O(log n) > O(n) > O(nlog n) > O(n²) > O(2ⁿ)
O(1)
- input data의 크기와 상관없이, 항상 일정한 시간이 걸림
- stack의 push, pop
bool function(vector<int> n){
if(n[0] == 0) return true;
return false;
}
O(log n)
- 실행시간이 입력크기의 Log에 비례
- quick sort, merge sort, heap sort, 이진트리
int function(key, vector<int> arr, first, last){
if(first > last) return -1;
int middle = (first + last) / 2;
if(arr[middle] > key) function(key, arr, first, middle - 1);
else if(arr[middle] < key) function(key, arr, middle + 1, last);
return middle;
}
O(n)
- input data의 크기에 비례하여 처리시간이 걸리는 알고리즘
- 최악의 경우 n개의 연산을 수행해야 할 경우 적용
- 반복문
void function(vector<int> n){
for(int i = 0; i < n.size(); i++){
cout << i;
}
}
O(n²)
- input data의 크기에 따라 시간효율성이 제곱으로 떨어짐
- 이중반복문, insertion sort, bubble sort, selectino sort
void function(vector<int> n){
for(int i = 0; i < n.size(); i++){
for(int j = 0; j < n.size(); j++){
cout << i+j;
}
}
}O(n³), ... ,O(nⁿ)
- 제곱이 늘어날수록 급격하게 처리시간이 늘어난다
- n중 반복문
O(2ⁿ)
- 지수형 표기법
- 지수적 증가는 연산횟수증가가 높음
- 피보나치 수열

vector function(int n, vector<int> m) {
if(n <= 0) return 0;
else if(n == 1) return m[n] = 1;
m[n] = function(n - 1, m) + function(n - 2, m)
return m;
}
'Computer Science > 알고리즘_자료구조' 카테고리의 다른 글
| [자료구조] BST(Binary Search Tree, 이진탐색트리) (0) | 2021.06.17 |
|---|---|
| [알고리즘] 위상 정렬(Topology Sort) (0) | 2021.06.01 |
| [자료구조] Doubly Linked List(2중 연결 리스트) (0) | 2021.05.20 |
| [자료구조] Hash Table (0) | 2021.05.14 |
| [자료구조] 2진트리 탐색 코드 (0) | 2021.04.20 |
