티스토리 뷰
최단경로 구하기
하나의 정점을 기준으로 다른 정점까지의 최단거리를 측정하는 알고리즘이다.
특정 지역에서 다른 지역까지의 최단 경로를 구하는 지도를 사용하는 application에서 사용할 수 있다.
node와 가중치(node 사이의 거리)가 있는 간선으로 표현되는 그래프에서 사용한다.
1번 노드에서 부터 6번 노드까지의 최단거리를 구해야 된다고 생각해보자.

모든 경우의 수에 대하여 계산해보자. (Brute force solution)
- 1 -> 2 -> 3 -> 4 -> 6 => 20
- 1 -> 2 -> 4 -> 6 => 15
- 1 -> 2 -> 5 -> 6 => 9
- 1 -> 3 -> 4 -> 6 => 13
최단경로는 3번째 경우의 수가 된다.
하지만 모든 경우의 수를 계산하는 방식은 시간이 많이 걸린다. => O(n²)
다익스트라 알고리즘
- dp를 활용한 최단경로 탐색 알고리즘이다.
- 시작노드와 연결된 다른 정점들의 거리를 업데이트 시켜준다.
- 시족 노드를 기준으로 각 노드의 최소 비용을 저장한다.
- 방문하지 않은 노드 중 가장 비용이 적은 노드를 선택한다.
- 해당 노드를 거쳐 특정한 노드로 가는 경우를 고려하여 최소비용을 갱신한다.
- 3 ~ 4를 반복한다.
1. 1번 노드에서 연결되어있는 노드간의 거리를 계산한다.

| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 1 | 3 | INF | INF | INF |
1번 노드는 자기자신이므로 0, 2번 노드는 1, 3번 노드는 3이 걸린다.
위의 상태를 고려하여 2번을 선택한다.
2. 2번 노드에서 그 다음 이동할 노드에 대한 거리를 계산한다.

| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 1 | 3 | 5 | 8 | INF |
1번 노드에서 3번 노드로 갈 수 있는 거리는 3이었다.
그리고 2번 노드에서 3번 노드를 갈 경우 1 + 6 = 7 이 나오는데 1번 노드에서 3번 노드로 바로가는 거리가 더 적으므로 3번의 내용은 유지시킨다.
이제 방문하지 않은 노드 중 가장 비용이 적게 드는 노드는 3이다.
3. 3번 노드에서 그 다음 이동할 노드에 대한 거리를 계산한다.
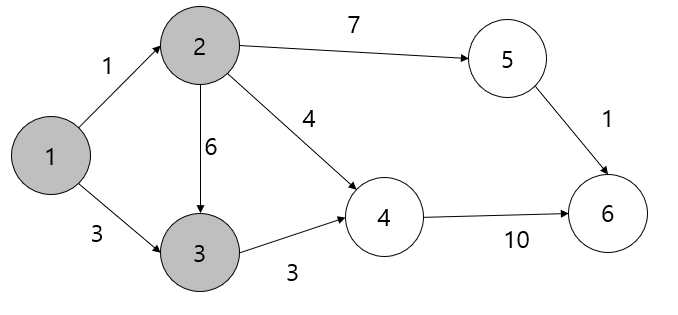
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 1 | 3 | 5 | 8 | INF |
4번 노드로 갈 때 3번 노드로 거쳐 가는 6보다 2번 노드로 거쳐가는 5가 더 작으므로 배열은 갱신하지 않는다.
4. 4번 노드에서 그 다음 이동할 노드에 대한 거리를 계산한다.

| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 1 | 3 | 5 | 8 | 15 |
4번 노드에서는 6번 노드로만 갈 수 있다.
15는 INF(무한)보다 작으므로 6번 노드로 가는 거리를 입력한다.
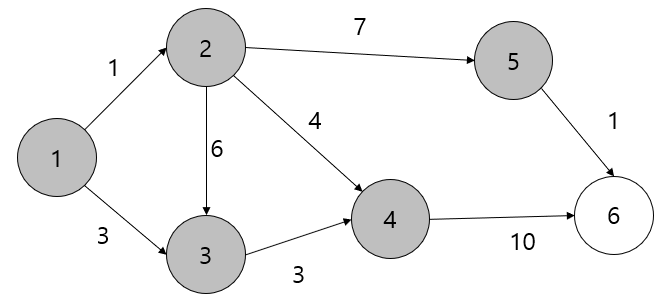
5. 5번 노드에서 그 다음 이동할 노드에 대한 거리를 계산한다.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 1 | 3 | 5 | 8 | 9 |
5번 노드에서는 6번 노드로의 이동만 가능하다.
5번 노드까지의 거리 8과 5번에서 6번으로의 거리 1은 9이며 이는 기존 15보다 작으므로 9로 갱신한다.

구현
다익스트라 알고리즘을 이용하여 문제를 풀어보자
https://www.acmicpc.net/problem/1753
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1≤V≤20,000, 1≤E≤300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1≤K≤V)가 주어진다.
www.acmicpc.net
C++ 코드
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
#define MAX 20001
#define INF 987654321
//node, dest, dist
vector<pair<int, int>> path[MAX];
int V, E, start;
void dijkstra(vector<int>& table) {
priority_queue<pair<int, int>> pq;
table[start] = 0;
pq.push(make_pair(0, start));
while (!pq.empty()) {
int cur = pq.top().second;
int weight = -pq.top().first;
pq.pop();
if (table[cur] < weight) continue;
for (int i = 0; i < path[cur].size(); i++) {
int connect = path[cur][i].first;
int conDist = weight + path[cur][i].second;
if (table[connect] > conDist) {
table[connect] = conDist;
pq.push(make_pair(-conDist, connect));
}
}
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
// node는 1부터 V까지
cin >> V >> E >> start;
for (int i = 0; i < E; i++) {
int u, v, w;
cin >> u >> v >> w;
path[u].push_back(make_pair(v, w));
}
V++;
vector<int> table(V, INF);
dijkstra(table);
for (int i = 1; i < V; i++) {
if (table[i] == INF) cout << "INF\n";
else cout << table[i] << "\n";
}
return 0;
}
Rust 코드
use std::io;
use std::collections::BinaryHeap;
struct Dijkstra {
max: usize,
inf: u32,
path: Vec<Vec<(u32, u32)>>,
v: usize,
e: u32,
start: usize,
table: Vec<u32>
}
impl Dijkstra {
fn new() -> Self {
Dijkstra {
max: 20001,
inf: 987654321,
path: vec![vec![]; 20001],
v: 0,
e: 0,
start: 0,
table: vec![]
}
}
fn dijkstra(&mut self) {
let mut pq = BinaryHeap::new();
self.table[self.start] = 0;
pq.push((0, self.start));
while let Some(unit) = pq.pop() {
let cur = unit.1;
let weight = -unit.0 as i32;
if (self.table[cur] as i32) < weight {
continue;
}
for i in 0..self.path[cur].len() {
let connect = self.path[cur][i].0;
let con_dist = weight + (self.path[cur][i].1 as i32);
if self.table[connect as usize] > con_dist as u32 {
self.table[connect as usize] = con_dist as u32;
pq.push((-con_dist, connect as usize))
}
}
}
}
fn input(&mut self) {
let mut input = String::new();
io::stdin().read_line(&mut input).expect("failure");
let tmp: Vec<&str> = input.split_whitespace().collect();
self.v = tmp[0].parse::<usize>().unwrap();
self.e = tmp[1].parse::<u32>().unwrap();
let mut input = String::new();
io::stdin().read_line(&mut input).expect("failure");
let tmp: Vec<&str> = input.split_whitespace().collect();
self.start = tmp[0].parse::<usize>().unwrap();
for i in 0..self.e {
let mut input = String::new();
io::stdin().read_line(&mut input).expect("failure");
let tmp: Vec<&str> = input.split_whitespace().collect();
let u = tmp[0].parse::<usize>().unwrap();
let v = tmp[1].parse::<u32>().unwrap();
let w = tmp[2].parse::<u32>().unwrap();
self.path[u].push((v, w));
}
self.v += 1;
self.table = vec![self.inf; self.v];
}
fn display(&self) {
for i in 1..self.v {
if self.table[i] == self.inf {
println!("INF\n");
}else{
println!("{}", self.table[i]);
}
}
}
}
1. 먼저 path배열에 node간 관계를 정리한다.
- index는 하나의 노드를 가리키며, 해당 노드에 연결되어 있는 노드와 거리(or 가중치)를 pair로 저장한다.
- 위에서 정리한 테이블을 예로들어보자
- 그럼 path배열에는 아래와 같이 저장이 된다.
- 1번째 index : [2, 1] , [3, 3]
- 2번째 index : [3, 6], [4, 4], [5, 7]
- 3번째 index : [4, 3]
- 4번째 index : [6, 10]
- 5번째 index : [6, 1]
- 6번째 index : []
2. 그 다음 각 노드별 계산한 거리를 저장할 table 배열을 생성한다. 초기값은 INF로 통일한다.
3. path배열과 table 배열을 이용하여 다익스트라 알고리즘을 실행한다.
- 현재 노드에서 가까운(or 가중치가 적은) 순서대로 처리하기 위해 priority_queue를 사용한다.
- 방문하고자 하는 노드와의 거리, 방문하고자하는 노드 형태의 pair타입으로 priority_queue를 정의한다.
- priority_queue는 내림차순으로 정렬된다. 거리가 짧은 노드가 큐의 가장 앞에 오도록 음수로 저장한다.
- 만약 다음 노드와의 거리가 1 과 3이 있을때, 그대로 저장하면 큐에 3, 1 순서대로 저장이 된다. 이를 역순으로 하기 위하여 음수로 저장할 필요가 있다. 음수로 저장할 경우 -1, -3 순서대로 저장이 되므로 음수로 저장한다.
- 그 다음 table[다음노드]의 거리를 갱신한다.
- 모든 거리가 계산이 되면 완성된 table을 출력한다.

Time Complexity : O(logN)
Space Complexity : O(N)
'Computer Science > 알고리즘_자료구조' 카테고리의 다른 글
| Greedy algorithm, 탐욕법 (0) | 2022.02.26 |
|---|---|
| 페이지 교체 알고리즘, Page replacement algorithm (0) | 2021.09.25 |
| [알고리즘] 정렬알고리즘(2) - bubble sort, 버블정렬 (0) | 2021.09.04 |
| [알고리즘] 문자열_알고리즘 KMP 알고리즘 (0) | 2021.08.28 |
| [알고리즘] 정렬 알고리즘(1) - selection sort, 선택정렬 (0) | 2021.07.02 |
